Random matek példák érettségire #3

A Random matek példák érettségire sorozatunk következő részben a 2010. évi tavaszi érettségi 14. feladatát fogjuk megoldani. A feladat megoldásához mindenképpen érdemes használni a függvénytáblázatot, hiszen minden fontos képlet megtalálható benne, amire szükségünk van.

Érdemes a feladat megoldása előtt egy koordinátarendszert felskiccelni, hogy lássuk, miről is van szó.

A feladat a.) részében az AB oldal oldalegyenesét kell felírnunk. Ehhez nyissuk ki a függvénytáblázatot a koordinátageometriát taglaló résznél. Itt meg fogjuk találni azt a részt, ami segít nekünk ennek az egyenesnek a felírásában.

Ha adott $P_{{1}}(x_{{1}};y_{{1}})$ és $P_{{2}}(x_{{2}};y_{{2}})$ pontok, akkor a következő egyenletet tudjuk felírni:

$(y_{{2}}-y_{{1}})\cdot(x-x_{{1}})=(x_{{2}}-x_{{1}})\cdot(y-y_{{1}})$

Helyettesítsünk be, ha A(0;0) pontot $P_{{1}}(x_{{1}};y_{{1}})$ ponttal és B(-2;4) pontot $P_{{2}}(x_{{2}};y_{{2}})$ ponttal azonosítjuk. Ekkor az egyenletünk a következő lesz:

$(4-0)\cdot(x-0)=(-2-0)\cdot(y-0)$

$4\cdot x=-2\cdot y$

$2\cdot y=-4\cdot x$

$y=-2\cdot x$

A feladat b.) részében az ABC háromszög legnagyobb szögét kell meghatároznunk. Amit mindenképpen tudnunk kell a feladat megoldásához, az az, hogy egy háromszög legnagyobb szöge mindig a leghosszabb oldallal szemben van! Na de melyik a leghosszabb oldal? Számoljuk ki az összes oldalt és megtudjuk! Ha szemfülesek vagyunk, láthatjuk, hogy a c.) részhez is szükségünk lesz az oldalak hosszára, így nem számolunk feleslegesen.

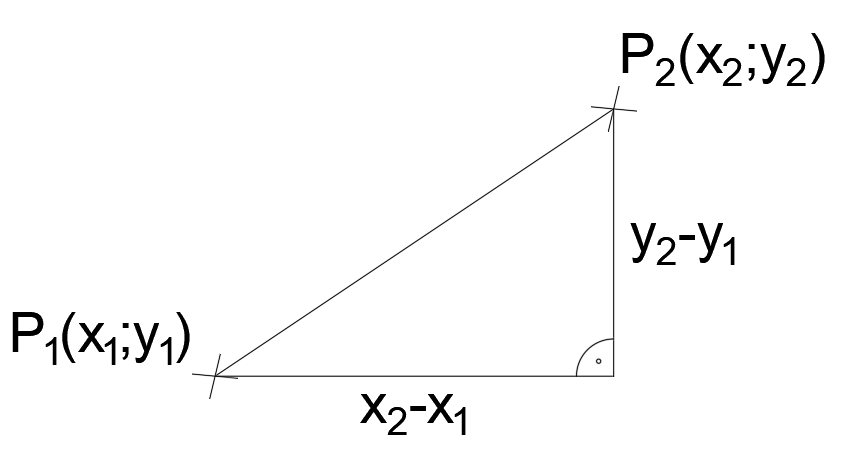
Két pont közötti egyenes hosszát úgy számoljuk ki, hogy a pontok megfelelő koordinátáit kivonjuk egymásból, a kapott eredményeket négyzetre emeljük, összeadjuk, majd gyököt vonunk az eredményből. Tulajdonképpen a Pitagorasz-tételt alkalmazzuk.

Vagyis:

$l=\sqrt{(x_{{2}}-x_{{1}})^2+(y_{2}-y_{{1}})^2$

Ez a képlet szintén szerepel a függvénytáblázatban, bármelyik két pont közötti egyenes hosszának a meghatározására alkalmas. Nézzük az oldalhosszakat a képlet alkalmazása után:

$AB=\sqrt{(-2-0)^2+(4-0)^2}=\sqrt{4+16}=\sqrt{20$

$BC=\sqrt{(4-(-2))^2+(5-4)^2}=\sqrt{36+1}=\sqrt{37$

$AC=\sqrt{(4-0)^2+(5-0)^2}=\sqrt{16+25}=\sqrt{41$

Az eredményekből látszik, hogy az AC oldal a leghosszabb, tehát az ezzel szemben lévő szög a legnagyobb.

A szög kiszámolására több megoldást is alkalmazhatunk. Mi most a koszinusz-tételt fogjuk felhasználni a megoldáshoz. A tétel így szól: bármely háromszögben az egyik oldal négyzetét megkapjuk, ha a másik két oldal négyzetének összegéből kivonjuk e két oldal és az általuk közbezárt szög koszinuszának kétszeres szorzatát.

Mivel a háromszögünk minden oldalát ismerjük, így a két oldal által közbezárt szög az AC oldallal szemközti szög legyen, vagyis a háromszög legnagyobb szöge, amit mi keresünk. Így a szög melletti oldalak az AB és BC oldalak lesznek.

$AC^{2}=AB^2+BC^2-2 \cdot AB \cdot BC \cdot cos\gamma$

$\sqrt{41}^{2}=\sqrt{20}^2+\sqrt{37}^2-2 \cdot \sqrt{20} \cdot \sqrt{37} \cdot cos\gamma$

$41=20+37-2 \cdot \sqrt{20} \cdot \sqrt{37} \cdot cos\gamma$

$41=57-2 \cdot \sqrt{20} \cdot \sqrt{37} \cdot cos\gamma$

$2 \cdot \sqrt{20} \cdot \sqrt{37} \cdot cos\gamma=16$

$cos\gamma=\frac{16}{2 \cdot \sqrt{20} \cdot \sqrt{37}}$

$cos\gamma=0,2941$

$\gamma=72,9$

A feladat c.) pontjában a háromszög területét kell kiszámolnunk, ami a fenti számítások után már gyerekjáték. 🙂 Felcsapjuk a függvénytáblázatot a geometria témakörénél, majd kikeressük a háromszög területének kiszámítását, ha fejből nem megy.

Használjuk fel a korábban kiszámolt szöget! A háromszög területét kiszámíthatjuk úgy is, hogy két oldal szorzatát megszorozzuk a közbezárt szög szinuszával, majd elosztjuk kettővel.

$T=\frac{AB \cdot BC \cdot sin\gamma}{{2}}$

$T=\frac{\sqrt{20} \cdot \sqrt{37}\cdot sin(72,9)}{{2}}$

$T=13$

Ez a feladat 12 pontos volt és szinte minden segítséget megkaptunk a függvénytáblázattól a megoldáshoz.

Jövünk vissza! 🙂