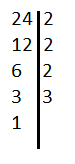 A legkisebb közös többszörös egy matematikai alapfogalom, melyet minden diáknak fontos ismernie. A korábbi érettségi feladatsorokban is előfordultak olyan példák, melyekben szükség volt a legkisebb közös többszörös fogalmának ismerete a feladat megoldásához.
A legkisebb közös többszörös egy matematikai alapfogalom, melyet minden diáknak fontos ismernie. A korábbi érettségi feladatsorokban is előfordultak olyan példák, melyekben szükség volt a legkisebb közös többszörös fogalmának ismerete a feladat megoldásához.
Lássuk akkor, hogy mi is a legkisebb közös többszörös fogalma “szaknyelven”: két pozitív egész szám esetén azt a legkisebb pozitív egész számot nevezzük a legkisebb közös többszörösnek, amely az adott két pozitív egész szám mindegyikével osztható. Tehát, ha van két szám előttem, akkor úgy tudom meghatározni a legkisebb közös többszörösüket, hogy megkeresem azt a legkisebb számot, amiben mindkettő osztható. Ugye egészen egyszerűnek hangzik? 🙂 Az is, azonban néhány kiegészítő dolgot mindenképpen tisztáznunk kell. Például, mi van akkor, ha a 254 és a 316 legkisebb közös többszörösét kell megtalálnom? Egészen hosszú ideig tartana megkeresni ezt a számot, ha nem ismernénk erre egy egyszerű megoldást, méghozzá egy szám prímtényezőkre való bontását. És arról még nem is esett szó, hogy mi van, ha több, mint két szám legkisebb közös többszörösét kell megkeresnünk…
Prímtényezőkre bontás
Mit is jelent az, hogy prím? Nagyon egyszerű ez a fogalom: olyan természetes számok, melyek csak eggyel és önmagukkal oszthatóak. Amikor prímtényezőkre bontunk egy számot, akkor prímszámokra bontjuk szét, például:
Bevett szokás, hogy függőleges vonallal elválasztva leírjuk az osztókat, a legkisebbtől a legnagyobb felé haladva egészen addig, amíg egyet kapunk az utolsó osztás során. Így a 24 prímtényezőkre felbontva a következőképpen néz ki: .
Legkisebb közös többszörös meghatározása
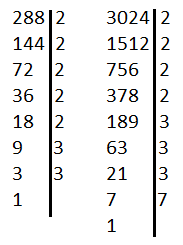
Keressük meg az alábbi két szám legkisebb közös többszörösét: [288;3024]. Amikor számok legkisebb közös többszörösét keressük, az adott számokat kapcsos zárójelben felírjuk – így jelezve, hogy mit szeretnénk meghatározni. Első lépésként a számokat prímtényezőkre bontjuk:
Így a számokat a következőképpen tudjuk felírni:
Ez az alak segít abban nekünk, hogy meghatározzuk a legkisebb közös többszöröst. Úgy tudjuk kiválasztani/meghatározni a legkisebb közös többszöröst, hogy először megkeressük az összes olyan prímtényezőt, amely mindkét számban megtalálható, a fenti esetben a 2, 3 és a 7. Majd ezeknek a legnagyobb hatványú előfordulását vesszük figyelembe. A 2 az ötödik és a negyedik hatványon is szerepel, tehát az ötödik hatványt vesszük figyelembe, mert az a nagyobb, a 3 a második és a harmadik hatványon is szerepel, így a harmadik hatványt vesszük figyelembe, mert az a nagyobb, a 7 az első hatványon szerepel, így értelemszerűen azt választjuk ki. Tehát a legkisebb közös többszörös:
Ha kettőnél több szám esetében kell meghatároznunk a legkisebb közös többszöröst, akkor is a fenti módszerrel járunk el.
Határozd meg a következő számok legkisebb közös többszörösét gyakorlásként!
[12;54]
[24;30]
[252;270]
[360;980]